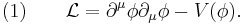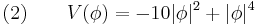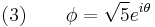Spontaneous symmetry breaking

Quantum field theory

History of...

Background
Gauge theory Field theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking

Symmetries
Crossing Charge conjugation Parity Time reversal

Tools
Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Renormalization Vacuum state Wick's theorem Wightman axioms

Equations
Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation

Standard Model
Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory

Incomplete theories
Quantum gravity String theory Supersymmetry Technicolor Theory of everything

Scientists

Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg •Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Wilczek • Witten • Yang • Yukawa • Zimmermann • Zinn-Justin

Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in a non symmetrical state. Though the process by itself is interesting from a mathematical point of view, it is fairly simple. Its fame outside the scientific community stems from its use in the standard model of particle physics, one of the most fundamental theories of science. In the context of its use within the standard model, it is far more complicated (because the standard model itself is a complicated theory).

1 General definition
- 1.1 Formal point of view
2 Everyday example
3 Importance within the standard model
4 Technical usage within physics
5 Mathematical example: the Mexican hat potential
6 Other examples
7 Nobel Prize
8 See also
9 Notes
10 External links

General definition

For spontaneous symmetry breaking to occur, there must be a system in which there are several equally likely outcomes. The system as a whole is therefore symmetric with respect to these outcomes (if we consider any two outcomes, the probability is the same). However, if the system is sampled (i.e. if the system is actually used or interacted with in any way) a specific outcome must occur. Though we know the system as a whole is symmetric, we also know that it is never encountered with this symmetry, only in one specific state. Because one of the outcomes is always found with probability 1, and the others with probability 0, they are no longer symmetric. Hence, the symmetry is said to be spontaneously broken in that theory.

Formal point of view

When a theory is symmetric with respect to a symmetry group, but asserts that one element of the group is distinct, then spontaneous symmetry breaking has occurred. To be clear: the theory must not say which member is distinct, only that one is. From this point on the theory can be treated as if this element actually is distinct, with the proviso that any results found in this way must be re symmetrised, by taking the average of each of the elements of the group being distinct one.

Everyday example

A common example to help explain this phenomenon is a ball sitting on top of a hill. This ball is in a completely symmetric state. However, its state is unstable: the slightest perturbing force will cause the ball to roll down the hill in some particular direction. At that point, symmetry has been broken because the direction in which the ball rolled has a feature that distinguishes it from all other directions.

Importance within the standard model

Before spontaneous symmetry breaking, the Standard Model predicts the existence of all the required particles. However, some particles (the W and Z bosons) are massless, when in reality they have mass. Obviously, this is a major failing of the theory in that state. To overcome this, the Higgs mechanism uses spontaneous symmetry breaking to give these particle masses. It also predicts a new, as yet undetected particle, the Higgs boson. This particle is frequently mentioned within the media, as major experiments, such as those at CERN, are currently trying to find it. If the Higgs boson is not found, it will mean the Higgs mechanism and spontaneous symmetry breaking as they are currently used cannot be correct, and physicists must come up with a new model to explain the fundamental laws of nature. A more detailed presentation of this mechanism is given in the article on the Yukawa interaction, where it is shown how spontaneous symmetry breaking can be used to give mass to fermions.

Technical usage within physics

The crucial concept here is the order parameter. If there is a field (often a background field) which acquires an expectation value (not necessarily a vacuum expectation value) which is not invariant under the symmetry in question, we say that the system is in the ordered phase and the symmetry is spontaneously broken. This is because other subsystems interact with the order parameter which forms a "frame of reference" to be measured against, so to speak.

If a vacuum state obeys the initial symmetry then the system is said to be in the Wigner mode, otherwise it is in the Goldstone mode.

The symmetry group can be discrete, such as the space group of a crystal, or continuous (e.g., a Lie group), such as the rotational symmetry of space. However if the system contains only a single spatial dimension then only discrete symmetries may be broken in a vacuum state of the full quantum theory, although a classical solution may break a continuous symmetry.

Mathematical example: the Mexican hat potential

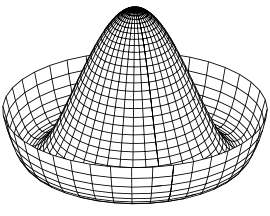
Graph of a Mexican hat potential function.

In the simplest example, the spontaneously broken field is described by a scalar field theory. In physics, one way of seeing spontaneous symmetry breaking is through the use of Lagrangians. Lagrangians, which essentially dictate how a system will behave, can be split up into kinetic and potential terms

$(1) \qquad \mathcal{L} = \partial^\mu \phi \partial_\mu \phi - V(\phi).$

It is in this potential term (V(φ)) that the action of symmetry breaking occurs. An example of a potential is illustrated in the graph at the right.

$(2) \qquad V(\phi) = -10|\phi|^2 + |\phi|^4 \,$

This potential has many possible minima (vacuum states) given by

$(3) \qquad \phi = \sqrt{5} e^{i\theta}$

for any real θ between 0 and 2π. The system also has an unstable vacuum state corresponding to Φ = 0. This state has a U(1) symmetry. However, once the system falls into a specific stable vacuum state (corresponding to a choice of θ) this symmetry will be lost or spontaneously broken.

Other examples

For ferromagnetic materials, the laws describing it are invariant under spatial rotations. Here, the order parameter is the magnetization, which measures the magnetic dipole density. Above the Curie temperature, the order parameter is zero, which is spatially invariant and there is no symmetry breaking. Below the Curie temperature, however, the magnetization acquires a constant (in the idealized situation where we have full equilibrium; otherwise, translational symmetry gets broken as well) nonzero value which points in a certain direction. The residual rotational symmetries which leaves the orientation of this vector invariant remain unbroken but the other rotations get spontaneously broken.
The laws describing a solid are invariant under the full Euclidean group, but the solid itself spontaneously breaks this group down to a space group. The displacement and the orientation are the order parameters.
The laws of physics are spatially invariant, but here on the surface of the Earth, we have a background gravitational field (which plays the role of the order parameter here) which points downwards, breaking the full rotational symmetry. This explains why up and down directions are "different" but all the horizontal directions are still isotropic.
General relativity has a Lorenz gauge symmetry, but in FRW cosmological models, the mean 4-velocity field defined by averaging over the velocities of the galaxies (the galaxies act like gas particles at cosmological scales) acts as an order parameter breaking this symmetry. Similar comments can be made about the cosmic microwave background.
Here on Earth, Galilean invariance (in the nonrelativistic approximation) is broken by the velocity field of the Earth/atmosphere, which acts as the order parameter here. This explains why people thought moving bodies tend towards rest before Galileo. We tend not to be aware of broken symmetries.
For the electroweak model, as explained earlier, the Higgs field acts as the order parameter breaking the electroweak gauge symmetry to the electromagnetic gauge symmetry. Like the ferromagnetic example, there is a phase transition at the electroweak temperature. The same comment about us not tending to notice broken symmetries explains why it took so long for us to discover electroweak unification.
For superconductors, there is a collective condensed matter field ψ which acts as the order parameter breaking the electromagnetic gauge symmetry.
In general relativity, diffeomorphism covariance is broken by the nonzero order parameter, the metric tensor field.
Take a flat plastic ruler which is identical on both sides and push both ends together. Before buckling, the system is symmetric under the reflection about the plane of the ruler. But after buckling, it either buckles upwards or downwards.
Consider a uniform layer of fluid over an infinite horizontal plane. This system has all the symmetries of the Euclidean plane. But now heat the bottom surface uniformly so that it becomes much hotter than the upper surface. When the temperature gradient becomes large enough, convection cells will form, breaking the Euclidean symmetry.
Consider a bead on a circular hoop that is rotated about a vertical diameter. As the rotational velocity is increased gradually from rest, the bead will initially stay at its initial equilibrium point at the bottom of the hoop (intuitively stable, lowest gravitational potential). At a certain critical rotational velocity, this point will become unstable and the bead will jump to one of two other newly created equilibria, equidistant from the center. Initially, the system is symmetric with respect to the diameter, yet after passing the critical velocity, the bead must choose between the two new equilibrium points, thus breaking symmetry. Note: This can easily be tried at home with an electric drill, a marble, and a pot cover, (or any other combination you can think of) and is the two-dimensional, mechanical analogue of the symmetry breaking that occurs in the Higgs Boson field.

Nobel Prize

On October 7, 2008, the Royal Swedish Academy of Sciences awarded the 2008 Nobel Prize in Physics to two Japanese citizens and a Japanese-born American for their work in subatomic physics. American Yoichiro Nambu, 87, of the University of Chicago, won half of the prize for the discovery of the mechanism of spontaneous broken symmetry. Japanese physicists Makoto Kobayashi and Toshihide Maskawa shared the other half of the prize for discovering the origin of the broken symmetry.^[1] The trio shared the 10 million kronor (1.25 million USD) purse, as well as a diploma and an invitation to the prize ceremonies in Stockholm on December 10, 2008.

Notes

↑ The Nobel Foundation. "The Nobel Prize in Physics 2008". nobelprize.org. http://nobelprize.org/nobel_prizes/physics/laureates/2008/index.html. Retrieved January 15, 2008.